scipy.signal.freqs

scipy.signal.freqs(b, a, worN=None, plot=None)

Compute frequency response of analog filter.

Given the numerator b and denominator a of a filter, compute its frequency response:

        b[0]*(jw)**(nb-1) + b[1]*(jw)**(nb-2) + ... + b[nb-1]
H(w) = -------------------------------------------------------
        a[0]*(jw)**(na-1) + a[1]*(jw)**(na-2) + ... + a[na-1]

Parameters :

b : ndarray

Numerator of a linear filter.

a : ndarray

Denominator of a linear filter.

worN : {None, int}, optional

If None, then compute at 200 frequencies around the interesting parts of the response curve (determined by pole-zero locations). If a single integer, then compute at that many frequencies. Otherwise, compute the response at the angular frequencies (e.g. rad/s) given in worN.

plot : callable

A callable that takes two arguments. If given, the return parameters w and h are passed to plot. Useful for plotting the frequency response inside freqs.

Returns :

w : ndarray

The angular frequencies at which h was computed.

h : ndarray

The frequency response.

See also

freqz

Compute the frequency response of a digital filter.

Notes

Using Matplotlib’s “plot” function as the callable for plot produces unexpected results, this plots the real part of the complex transfer function, not the magnitude.

Examples

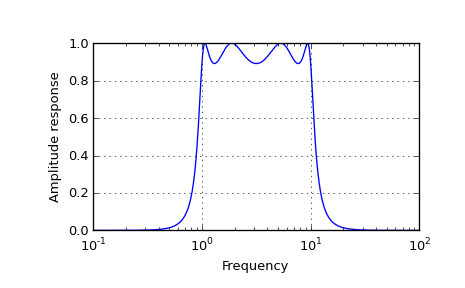
>>> from scipy.signal import freqs, iirfilter

>>> b, a = iirfilter(4, [1, 10], 1, 60, analog=True, ftype='cheby1')

>>> w, h = freqs(b, a, worN=np.logspace(-1, 2, 1000))

>>> import matplotlib.pyplot as plt
>>> plt.semilogx(w, abs(h))
>>> plt.xlabel('Frequency')
>>> plt.ylabel('Amplitude response')
>>> plt.grid()
>>> plt.show()

(Source code)