scipy.special.lambertw

scipy.special.lambertw(z, k=0, tol=1e-8)

Lambert W function.

The Lambert W function W(z) is defined as the inverse function of w * exp(w). In other words, the value of W(z) is such that z = W(z) * exp(W(z)) for any complex number z.

The Lambert W function is a multivalued function with infinitely many branches. Each branch gives a separate solution of the equation w exp(w). Here, the branches are indexed by the integer k.

Parameters :

z : array_like

Input argument.

k : int, optional

Branch index.

tol : float, optional

Evaluation tolerance.

Notes

All branches are supported by lambertw:

• lambertw(z) gives the principal solution (branch 0)
• lambertw(z, k) gives the solution on branch k

The Lambert W function has two partially real branches: the principal branch (k = 0) is real for real z > -1/e, and the k = -1 branch is real for -1/e < z < 0. All branches except k = 0 have a logarithmic singularity at z = 0.

Possible issues

The evaluation can become inaccurate very close to the branch point at -1/e. In some corner cases, lambertw might currently fail to converge, or can end up on the wrong branch.

Algorithm

Halley’s iteration is used to invert w * exp(w), using a first-order asymptotic approximation (O(log(w)) or O(w)) as the initial estimate.

The definition, implementation and choice of branches is based on [R114].

TODO: use a series expansion when extremely close to the branch point at -1/e and make sure that the proper branch is chosen there

References

[R114]

(1, 2) Corless et al, “On the Lambert W function”, Adv. Comp. Math. 5 (1996) 329-359. http://www.apmaths.uwo.ca/~djeffrey/Offprints/W-adv-cm.pdf

Examples

The Lambert W function is the inverse of w exp(w):

>>> from scipy.special import lambertw
>>> w = lambertw(1)
>>> w
0.56714329040978387299996866221035555
>>> w*exp(w)
1.0

Any branch gives a valid inverse:

>>> w = lambertw(1, k=3)
>>> w
(-2.8535817554090378072068187234910812 +
17.113535539412145912607826671159289j)
>>> w*exp(w)
(1.0 + 3.5075477124212226194278700785075126e-36j)

Applications to equation-solving

The Lambert W function may be used to solve various kinds of equations, such as finding the value of the infinite power tower :

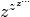>>> def tower(z, n):
... if n == 0:
... return z
... return z ** tower(z, n-1)
...
>>> tower(0.5, 100)
0.641185744504986
>>> -lambertw(-log(0.5))/log(0.5)
0.6411857445049859844862004821148236665628209571911

Properties

The Lambert W function grows roughly like the natural logarithm for large arguments:

>>> lambertw(1000)
5.2496028524016
>>> log(1000)
6.90775527898214
>>> lambertw(10**100)
224.843106445119
>>> log(10**100)
230.258509299405

The principal branch of the Lambert W function has a rational Taylor series expansion around z = 0:

>>> nprint(taylor(lambertw, 0, 6), 10)

[0.0, 1.0, -1.0, 1.5, -2.666666667, 5.208333333, -10.8]

Some special values and limits are:

>>> lambertw(0)
0.0
>>> lambertw(1)
0.567143290409784
>>> lambertw(e)
1.0
>>> lambertw(inf)
+inf
>>> lambertw(0, k=-1)
-inf
>>> lambertw(0, k=3)
-inf
>>> lambertw(inf, k=3)
(+inf + 18.8495559215388j)

The k = 0 and k = -1 branches join at z = -1/e where W(z) = -1 for both branches. Since -1/e can only be represented approximately with mpmath numbers, evaluating the Lambert W function at this point only gives -1 approximately:

>>> lambertw(-1/e, 0)
-0.999999999999837133022867
>>> lambertw(-1/e, -1)
-1.00000000000016286697718

If -1/e happens to round in the negative direction, there might be a small imaginary part:

>>> lambertw(-1/e)
(-1.0 + 8.22007971511612e-9j)