Fourier Transforms (scipy.fftpack)¶
Warning
This is currently a stub page
Contents
Fourier analysis is fundamentally a method for expressing a function as a sum of periodic components, and for recovering the signal from those components. When both the function and its Fourier transform are replaced with discretized counterparts, it is called the discrete Fourier transform (DFT). The DFT has become a mainstay of numerical computing in part because of a very fast algorithm for computing it, called the Fast Fourier Transform (FFT), which was known to Gauss (1805) and was brought to light in its current form by Cooley and Tukey [CT]. Press et al. [NR] provide an accessible introduction to Fourier analysis and its applications.
One dimensional discrete Fourier transforms¶
fft, ifft, rfft, irfft
Two and n dimensional discrete Fourier transforms¶
fft in more than one dimension
Discrete Cosine Transforms¶
Return the Discrete Cosine Transform [Mak] of arbitrary type sequence x.
For a single dimension array x, dct(x, norm='ortho') is equal to MATLAB dct(x).
There are theoretically 8 types of the DCT [WP], only the first 3 types are implemented in scipy. ‘The’ DCT generally refers to DCT type 2, and ‘the’ Inverse DCT generally refers to DCT type 3.
type I¶
There are several definitions of the DCT-I; we use the following (for norm=None):
![\[ y_k = x_0 + (-1)^k x_{N-1} + 2\sum_{n=1}^{N-2} x_n
\cos\left({\pi nk\over N-1}\right),
\qquad 0 \le k < N. \]](../_images/math/48f3da0bab41b09706ae0602c33cbd9ab398f428.png)
Only None is supported as normalization mode for DCT-I. Note also that the DCT-I is only supported for input size > 1
type II¶
There are several definitions of the DCT-II; we use the following (for norm=None):
![\[ y_k = 2 \sum_{n=0}^{N-1} x_n
\cos \left({\pi(2n+1)k \over 2N} \right)
\qquad 0 \le k < N.\]](../_images/math/be705fbc486ef12ed8709bc2bbbad5b7e3b6c307.png)
If norm='ortho',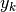 
is multiplied by a scaling factor f:
![\[f = \begin{cases} \sqrt{1/(4N)}, & \text{if $k = 0$} \\
\sqrt{1/(2N)}, & \text{otherwise} \end{cases} \]](../_images/math/8539deace9df2375e18b7a069dd78f89d3e9faea.png)
Which makes the corresponding matrix of coefficients orthonormal (OO’ = Id).
type III¶
There are several definitions, we use the following (for norm=None):
![\[ y_k = x_0 + 2 \sum_{n=1}^{N-1} x_n
\cos\left({\pi n(2k+1) \over 2N}\right)
\qquad 0 \le k < N,\]](../_images/math/340490f784c338bc97bb2c9f66e1059c4111cf0e.png)
or, for norm='ortho':
![\[ y_k = {x_0\over\sqrt{N}} + {1\over\sqrt{N}} \sum_{n=1}^{N-1}
x_n \cos\left({\pi n(2k+1) \over 2N}\right)
\qquad 0 \le k < N.\]](../_images/math/2b105080f0cefc2833d91049830098acbb1727ac.png)
The (unnormalized) DCT-III is the inverse of the (unnormalized) DCT-II, up to a factor 2N. The orthonormalized DCT-III is exactly the inverse of the orthonormalized DCT-II.
References¶
| [CT] | Cooley, James W., and John W. Tukey, 1965, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19: 297-301. |
| [NR] | Press, W., Teukolsky, S., Vetterline, W.T., and Flannery, B.P., 2007, Numerical Recipes: The Art of Scientific Computing, ch. 12-13. Cambridge Univ. Press, Cambridge, UK. |
| [Mak] | J. Makhoul, 1980, ‘A Fast Cosine Transform in One and Two Dimensions’, IEEE Transactions on acoustics, speech and signal processing vol. 28(1), pp. 27-34, http://dx.doi.org/10.1109/TASSP.1980.1163351 |
| [WP] | http://en.wikipedia.org/wiki/Discrete_cosine_transform |
FFT convolution¶
scipy.fftpack.convolve performs a convolution of two one-dimensional arrays in frequency domain.
Table Of Contents
Previous topic
Interpolation (scipy.interpolate)
Next topic
Signal Processing (scipy.signal)