numpy.polynomial.polynomial.polyfromroots

numpy.polynomial.polynomial.polyfromroots(roots)

Generate a monic polynomial with given roots.

Return the coefficients of the polynomial

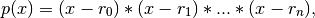
where the r_n are the roots specified in roots. If a zero has multiplicity n, then it must appear in roots n times. For instance, if 2 is a root of multiplicity three and 3 is a root of multiplicity 2, then roots looks something like [2, 2, 2, 3, 3]. The roots can appear in any order.

If the returned coefficients are c, then

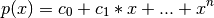
The coefficient of the last term is 1 for monic polynomials in this form.

Parameters :

roots : array_like

Sequence containing the roots.

Returns :

out : ndarray

1-D array of the polynomial’s coefficients If all the roots are real, then out is also real, otherwise it is complex. (see Examples below).

See also

chebfromroots, legfromroots, lagfromroots, hermfromroots, hermefromroots

Notes

The coefficients are determined by multiplying together linear factors of the form (x - r_i), i.e.

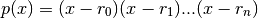
where n == len(roots) - 1; note that this implies that 1 is always returned for .

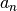Examples

>>> import numpy.polynomial as P
>>> P.polyfromroots((-1,0,1)) # x(x - 1)(x + 1) = x^3 - x
array([ 0., -1.,  0.,  1.])
>>> j = complex(0,1)
>>> P.polyfromroots((-j,j)) # complex returned, though values are real
array([ 1.+0.j,  0.+0.j,  1.+0.j])