numpy.i0

numpy.i0(x)

Modified Bessel function of the first kind, order 0.

Usually denoted 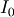. This function does broadcast, but will not “up-cast” int dtype arguments unless accompanied by at least one float or complex dtype argument (see Raises below).

Parameters:

x : array_like, dtype float or complex

Argument of the Bessel function.

Returns:

out : ndarray, shape = x.shape, dtype = x.dtype

The modified Bessel function evaluated at each of the elements of x.

Raises:

TypeError: array cannot be safely cast to required type :

If argument consists exclusively of int dtypes.

See also

scipy.special.iv, scipy.special.ive

Notes

We use the algorithm published by Clenshaw [R38] and referenced by Abramowitz and Stegun [R39], for which the function domain is partitioned into the two intervals [0,8] and (8,inf), and Chebyshev polynomial expansions are employed in each interval. Relative error on the domain [0,30] using IEEE arithmetic is documented [R40] as having a peak of 5.8e-16 with an rms of 1.4e-16 (n = 30000).

References

[R38]

(1, 2) C. W. Clenshaw, “Chebyshev series for mathematical functions,” in National Physical Laboratory Mathematical Tables, vol. 5, London: Her Majesty’s Stationery Office, 1962.

[R39]

(1, 2) M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, 10th printing, New York: Dover, 1964, pp. 379. http://www.math.sfu.ca/~cbm/aands/page_379.htm

[R40]

(1, 2) http://kobesearch.cpan.org/htdocs/Math-Cephes/Math/Cephes.html

Examples

>>> np.i0([0.])
array(1.0)
>>> np.i0([0., 1. + 2j])
array([ 1.00000000+0.j        ,  0.18785373+0.64616944j])