numpy.fft.fft

numpy.fft.fft(a, n=None, axis=-1)

Compute the one-dimensional discrete Fourier Transform.

This function computes the one-dimensional n-point discrete Fourier Transform (DFT) with the efficient Fast Fourier Transform (FFT) algorithm [CT].

Parameters:

a : array_like

Input array, can be complex.

n : int, optional

Length of the transformed axis of the output. If n is smaller than the length of the input, the input is cropped. If it is larger, the input is padded with zeros. If n is not given, the length of the input (along the axis specified by axis) is used.

axis : int, optional

Axis over which to compute the FFT. If not given, the last axis is used.

Returns:

out : complex ndarray

The truncated or zero-padded input, transformed along the axis indicated by axis, or the last one if axis is not specified.

Raises:

IndexError :

if axes is larger than the last axis of a.

See also

numpy.fft

for definition of the DFT and conventions used.

ifft

The inverse of fft.

fft2

The two-dimensional FFT.

fftn

The n-dimensional FFT.

rfftn

The n-dimensional FFT of real input.

fftfreq

Frequency bins for given FFT parameters.

Notes

FFT (Fast Fourier Transform) refers to a way the discrete Fourier Transform (DFT) can be calculated efficiently, by using symmetries in the calculated terms. The symmetry is highest when n is a power of 2, and the transform is therefore most efficient for these sizes.

The DFT is defined, with the conventions used in this implementation, in the documentation for the numpy.fft module.

References

[CT]	Cooley, James W., and John W. Tukey, 1965, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19: 297-301.

Examples

>>> np.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([ -3.44505240e-16 +1.14383329e-17j,
         8.00000000e+00 -5.71092652e-15j,
         2.33482938e-16 +1.22460635e-16j,
         1.64863782e-15 +1.77635684e-15j,
         9.95839695e-17 +2.33482938e-16j,
         0.00000000e+00 +1.66837030e-15j,
         1.14383329e-17 +1.22460635e-16j,
         -1.64863782e-15 +1.77635684e-15j])

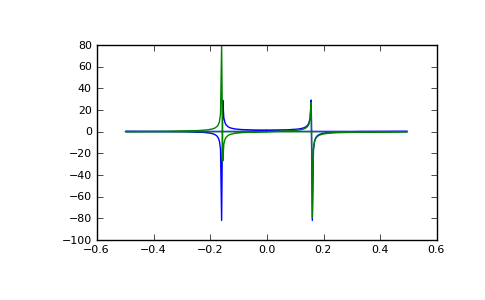
>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
>>> sp = np.fft.fft(np.sin(t))
>>> freq = np.fft.fftfreq(t.shape[-1])
>>> plt.plot(freq, sp.real, freq, sp.imag)
>>> plt.show()

In this example, real input has an FFT which is Hermitian, i.e., symmetric in the real part and anti-symmetric in the imaginary part, as described in the numpy.fft documentation.

(Source code)

Output

(png, pdf)