numpy.invert

numpy.invert(x[, out])

Compute bit-wise inversion, or bit-wise NOT, element-wise.

When calculating the bit-wise NOT of an element x, each element is first converted to its binary representation (which works just like the decimal system, only now we’re using 2 instead of 10):

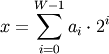
where W is the bit-width of the type (i.e., 8 for a byte or uint8), and each 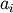is either 0 or 1. For example, 13 is represented as 00001101, which translates to .

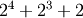The bit-wise operator is the result of

where is the NOT operator, which yields 1 whenever 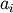is 0 and yields 0 whenever 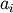is 1.

For signed integer inputs, the two’s complement is returned. In a two’s-complement system negative numbers are represented by the two’s complement of the absolute value. This is the most common method of representing signed integers on computers [40]. A N-bit two’s-complement system can represent every integer in the range 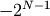to .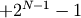

Parameters:

x1 : ndarray

Only integer types are handled (including booleans).

Returns:

out : ndarray

Result.

See also

bitwise_and, bitwise_or, bitwise_xor, logical_not

binary_repr

Return the binary representation of the input number as a string.

Notes

bitwise_not is an alias for invert:

>>> np.bitwise_not is np.invert
True

References

[40]	Wikipedia, “Two’s complement”, http://en.wikipedia.org/wiki/Two’s_complement

Examples

We’ve seen that 13 is represented by 00001101. The invert or bit-wise NOT of 13 is then:

>>> np.invert(np.array([13], dtype=uint8))
array([242], dtype=uint8)
>>> np.binary_repr(x, width=8)
'00001101'
>>> np.binary_repr(242, width=8)
'11110010'

The result depends on the bit-width:

>>> np.invert(np.array([13], dtype=uint16))
array([65522], dtype=uint16)
>>> np.binary_repr(x, width=16)
'0000000000001101'
>>> np.binary_repr(65522, width=16)
'1111111111110010'

When using signed integer types the result is the two’s complement of the result for the unsigned type:

>>> np.invert(np.array([13], dtype=int8))
array([-14], dtype=int8)
>>> np.binary_repr(-14, width=8)
'11110010'

Booleans are accepted as well:

>>> np.invert(array([True, False]))
array([False,  True], dtype=bool)