numpy.bitwise_xor

numpy.bitwise_xor(x1, x2[, out])

Compute bit-wise XOR of two arrays, element-wise.

When calculating the bit-wise XOR between two elements, x and y, each element is first converted to its binary representation (which works just like the decimal system, only now we’re using 2 instead of 10):

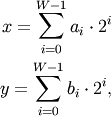
where W is the bit-width of the type (i.e., 8 for a byte or uint8), and each 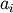and is either 0 or 1. For example, 13 is represented as 00001101, which translates to .

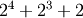The bit-wise operator is the result of

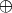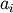where is the XOR operator, which yields one whenever either or 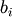is 1, but not both.

Parameters:

x1, x2 : array_like

Only integer types are handled (including booleans).

Returns:

out : ndarray

Result.

See also

bitwise_and, bitwise_or, logical_xor

binary_repr

Return the binary representation of the input number as a string.

Examples

We’ve seen that 13 is represented by 00001101. Similary, 17 is represented by 00010001. The bit-wise XOR of 13 and 17 is therefore 00011100, or 28:

>>> np.bitwise_xor(13, 17)
28
>>> np.binary_repr(28)
'11100'

>>> np.bitwise_xor(31, 5)
26
>>> np.bitwise_xor([31,3], 5)
array([26,  6])

>>> np.bitwise_xor([31,3], [5,6])
array([26,  5])
>>> np.bitwise_xor([True, True], [False, True])
array([ True, False], dtype=bool)