numpy.linalg.pinv¶
- numpy.linalg.pinv(a, rcond=1e-15)[source]¶
Compute the (Moore-Penrose) pseudo-inverse of a matrix.
Calculate the generalized inverse of a matrix using its singular-value decomposition (SVD) and including all large singular values.
Parameters: a : (M, N) array_like
Matrix to be pseudo-inverted.
rcond : float
Cutoff for small singular values. Singular values smaller (in modulus) than rcond * largest_singular_value (again, in modulus) are set to zero.
Returns: B : (N, M) ndarray
The pseudo-inverse of a. If a is a matrix instance, then so is B.
Raises: LinAlgError
If the SVD computation does not converge.
Notes
The pseudo-inverse of a matrix A, denoted
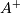 , is
defined as: “the matrix that ‘solves’ [the least-squares problem]
, is
defined as: “the matrix that ‘solves’ [the least-squares problem]
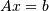 ,” i.e., if
,” i.e., if  is said solution, then
is said solution, then
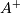 is that matrix such that
is that matrix such that 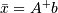 .
.It can be shown that if
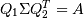 is the singular
value decomposition of A, then
is the singular
value decomposition of A, then
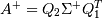 , where
, where 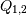 are
orthogonal matrices,
are
orthogonal matrices, 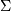 is a diagonal matrix consisting
of A’s so-called singular values, (followed, typically, by
zeros), and then
is a diagonal matrix consisting
of A’s so-called singular values, (followed, typically, by
zeros), and then 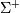 is simply the diagonal matrix
consisting of the reciprocals of A’s singular values
(again, followed by zeros). [R42]
is simply the diagonal matrix
consisting of the reciprocals of A’s singular values
(again, followed by zeros). [R42]References
[R42] (1, 2) G. Strang, Linear Algebra and Its Applications, 2nd Ed., Orlando, FL, Academic Press, Inc., 1980, pp. 139-142. Examples
The following example checks that a * a+ * a == a and a+ * a * a+ == a+:
>>> a = np.random.randn(9, 6) >>> B = np.linalg.pinv(a) >>> np.allclose(a, np.dot(a, np.dot(B, a))) True >>> np.allclose(B, np.dot(B, np.dot(a, B))) True
